来自斯坦福大学于2017年发表的论文，该网络为从对象分类、部件分割到场景语义分析的各种应用提供了统一的体系结构。虽然简单，但PointNet是高效和有效的。从经验来看，它表现出与最先进水平持平甚至更好的强劲表现。理论上，这篇论文提供了关于了解网络学习了什么，以及为什么网络对于输入扰动和破坏是健壮的分析。
Introduction
第一段简单地说明了以往研究人员处理点云数据的方式以及这种方式的缺陷。
在本文中，我们探索了能够对点云或网格(meshes)等3D几何数据进行推理的深度学习体系结构。典型的卷积体系结构需要高度规则的输入数据格式，如图像网格或3D体素的格式，以便执行权重分担和其他内核优化。由于点云或网格不是规则格式，大多数研究人员通常将这些数据转换为规则的3D体素网格或图像集合(例如，视图)，然后再将其提供给深层网络体系结构。然而，这种数据表示转换使结果数据变得不必要地庞大，同时还引入了量化伪像，这可能会模糊数据的自然不变性。
第二段讲述了本文的研究重点
出于这个原因，我们将重点放在使用简单的点云来表示3D几何形状上-并将产生的深层网络命名为PointNets。点云是一种简单而统一的结构，避免了网格（meshes)的组合不规则性和复杂性，因此更容易学习。但我们仍然必须尊重这样一个事实，即点云只是一组点，因此不随其成员的排列而变化，从而需要在网络计算中进行某些对称化。还需要考虑刚性运动的进一步不变性。
第三段介绍了网络的基本结构
我们的PointNet是一个统一的架构，它直接将点云作为输入，并为整个输入输出类标签，或为输入的每个点输出每个点段/部分的标签。我们网络的基本架构出人意料地简单，因为在初始阶段，每个点都是以相同和独立的方式处理的。在基本设置中，每个点仅由其三个坐标(x，y，z)表示。可以通过计算法线和其他局部或全局特征来添加附加维度
第四段介绍了网络的关键实现
我们方法的关键是使用单个对称函数max pooling。网络有效地学习一组优化函数/标准，该优化函数/标准选择点云的感兴趣或信息点，并对选择它们的原因进行编码。网络的最终完全连接层将这些学习到的最佳值聚集到上述整个形状的全局描述符中(形状分类)，或者用于预测每个点的标签(形状分割)。
后面几段都是一些网络的好处，总的来说，这篇文章的贡献在于：
Contribution
- 设计了一种适用于三维无序点集的深度网络体系结构；
- 我们展示了如何训练这样的网络来执行3D形状分类、形状部分分割和场景语义分析任务；
- 我们对该方法的稳定性和有效性进行了深入的经验和理论分析；
- 我们展示了由网络中选定的神经元计算的3D特征，并对其性能进行了直观的解释。
Related work
Point Cloud Feature
点云特征：所谓特征，就是能够表达出同类事物的一个统一表述。对于点云而言，相同表面或者相似表面上的点的特征应该非常相似。一个良好的点云特征不应该受刚性变换，采样密度以及轻微噪声的影响。
大多数现有的点云特征都是针对特定任务手工创建的。点特征通常是点的某些统计学性质的编码，并且它们设计成对某些变换具有不变性。这些变换通常被分类为内在的，或外部的。它们还可以分为局部特征和全局特征。对于特定的任务，找到最优的特征组合并不是一件容易的事。
手工创建的：即人工标注出感兴趣的信息，这类特征一般都是符合直觉的，但是有时候难免会有疏漏和想当然的成分。
Deep Learning on 3D data
这是直接使用3D数据进行深度学习的方法。3D数据有多种流行的表示法，这导致了不同的学习方法。
Volumetric CNNs*：是将3D卷积神经网络应用于体素形状的先驱。然而，由于*三维卷积的数据稀疏性和计算代价，体表示受到其分辨率的限制。FPNN和Vote3D提出了处理稀疏性问题的特殊方法,然而他们的操作仍然是在稀疏的体积上，这对他们来说处理非常大的点云是具有挑战性的*。
Multiview CNNs*：尝试*将3D点云或形状绘制成2D图像*，然后应用2D ConvNet对其进行分类。利用设计良好的图像CNN，这一系列方法在形状分类和检索任务上取得了很好的性能。然而，将它们扩展到场景理解或其他3D任务(如点分类和形状完成)并不是一件容易的事情。
Spectral CNNs*：一些最新的工作在网格上使用Spectral CNNs*。然而，这些方法目前仅限于多种网格，如有机对象，如何将其扩展到非等轴测形状，如家具，并不明显。
***Feature-based DNNs：***首先通过提取传统的形状特征将3D数据转换为向量，然后使用全连通网络对形状进行分类。我们认为它们受到提取的特征的表示能力的限制。
Deep Learning on Unordered Sets
对无序点集进行深度学习，可以这样做是因为：从数据结构的角度来看，点云是一组无序的矢量。
虽然大多数深度学习的工作都集中在规则的输入表示上，如序列(语音和语言处理)、图像和体积(视频或3D数据)，但在点集的深度学习方面却没有做太多的工作。Oriol Vinyals等人最近的一项研究探讨了这个问题。他们使用一个带有注意机制的读-处理-写网络来处理无序的输入集，并表明他们的网络具有对数字进行排序的能力。然而，由于他们的工作主要集中在一般集合和NLP应用上，因此缺乏几何在集合中的作用。
Problem statement
我们设计了一个直接使用无序点集作为输入的深度学习框架。点云被表示为一组三维点 {Pi|i=1,…,n} ，其中每个点 Pi 是其 (x,y,z) 坐标加上额外特征通道(如颜色、法线等)的矢量。为简单和清晰起见，除非另有说明，否则我们仅使用 (x,y,z) 坐标作为点的通道。
对于对象分类任务，输入点云要么直接从形状中采样，要么从场景点云中预分割。我们提出的网络对于每个候选类都输出一个分数。对于语义分割，输入可以是用于部分区域分割的单个对象，或者用于对象区域分割的3D场景的子体积。我们的模型将为n个点和m个语义子类别中共输出 n×m 个分数。
Deep Learning On Point Sets
Properties of Point Sets in Rn
网络的输入是来自欧氏空间的点的子集，具有以下的特性
- 无序性
与图像中的像素阵列或体积网格中的体素阵列不同，点云是一组没有特定顺序的点。换句话说，一个包含 N 个点的3D点云需要对 N! 种点的输入顺序保持一致性（不变性）
保持一致性：不管怎么输入，都应该是原来那个点云
- 点之间的相互作用
这些点来自具有距离度量的空间。这意味着点不是孤立的，相邻的点形成一个有意义的子集。因此，模型需要能够从邻近的点捕捉局部结构，以及局部结构之间的组合相互作用。
- 变换下的不变性
作为一个几何对象，学习的点集表示对于某些变换应该是不变的。例如，同时旋转和平移点不应修改全局点云类别或点的分割。
网络结构
整个网络的结构如下
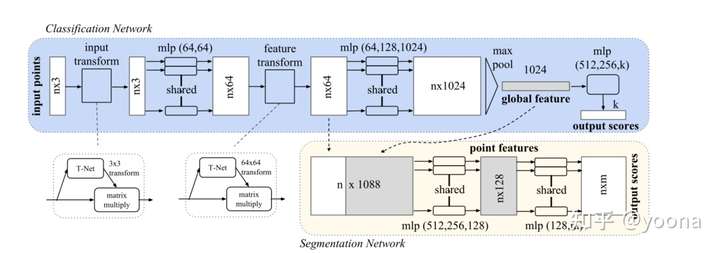该分类网络以n个点为输入，进行输入和特征变换，然后聚合点的特征。输出结果是k个类别的分数。用作语义分割的网络是分类网络的扩展，它将全局和局部特征连在一起，输出每个点的分数。“MLP”代表多层感知器，括号中的数字是层的大小。BatchNorm用于具有RELU的所有层。dropout层被用于mlp分类网络一层。
该网络有三个关键模块：
- 作为从所有点聚合信息的对称函数的最大池化层
- 组合局部信息和全局信息的结构
- 将输入点和点特征对齐的结构
下面我们将一一讲解这些结构以及其被这样设计的理由：
作为从所有点聚合信息的对称函数的最大池化层
首先为了使模型对输入排列保持不变，存在三种策略
1)将输入按规范顺序排序；
虽然排序听起来像是一个简单的解决方案，但在高维空间中，但在高维空间中，实际上并不存在一般意义上相对于点扰动稳定的排序。
2）将输入视为训练RNN的序列
这种想法将点集考虑成序列信号，并用随机的序列训练RNN，希望最终的RNN可以对输入顺序保持不变性。在“OrderMatters”一书中，作者证明了顺序确实很重要，不能完全省略，但是RNN只能对于长度较小(几十个)的序列的输入排序具有相对较好的鲁棒性，却很难扩展到数千个输入元素，这是点集的常见大小。
3）使用一个简单的对称函数来聚合每个点的信息
我们的想法是通过 对集合中变换的元素 应用对称函数 来近似定义 在点集上的一般函数
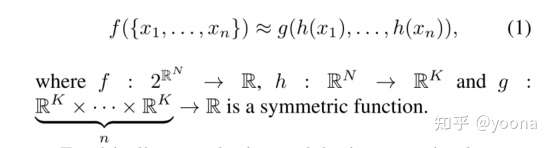
通过MLP来近似 h, g 由一个单变量函数和最大池化函数组合构成 。
在对称函数中，函数的输出值不随输入变数的排列而改变，
全局变量和局部变量的聚合
上述的模块输出的信息可以形成一个全局向量 [f1,…,fk] 。对于分类问题，我们可以简单地训练一个SVM或者多层感知机分类器。然而，对于分割问题，我们还需要全局特征和局部特征的聚合。
正如下图展示了我们的处理方法：
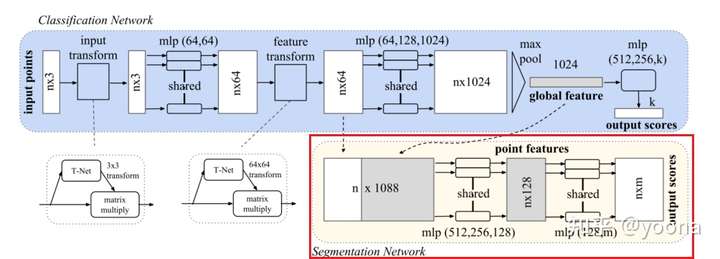
计算全局点云特征向量后，通过将全局特征与每个点特征连接起来，将其反馈给逐点特征。然后，我们基于组合点特征提取新的逐点特征–这一次，逐点特征同时知道局部和全局信息。
通过这种修改，我们的网络能够预测依赖于局部几何和全局语义的每个点的数量。例如，我们可以准确地预测每个点的法线，验证网络能够汇总来自点的局部邻域的信息。在实验环节中，我们还证明了该模型在形状部分分割和场景分割方面都能达到最好的性能。
输入点和点特征对齐
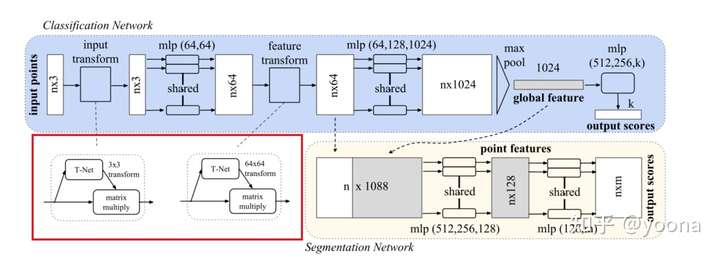
如果点云经过某些几何变换(如刚性变换)，则点云的语义标签必须是不变的。因此，我们期望通过我们的点集学习的表示对于这些变换是不变的。一种自然的解决方案是在特征提取之前将所有输入集合与规范空间对齐。Jaderberg等人引入了空间变换的思想，通过采样和内插来对齐2D图像，并在GPU上实现了一个专门定制的层。
与Jaderberg相比，我们的点云输入形式使我们能够以一种简单得多的方式实现这一目标。我们不需要发明任何新的层，也不会像在图像中那样引入别名。我们通过一个微型网络(下图t网络)预测一个仿射变换矩阵，并将该变换直接应用于输入点的坐标。微型网络本身类似于大网络，由点无关特征提取、最大集合和全连通层等基本模块组成。
在文中并没有详细的说明t网络的细节信息
Experiment
3D Object Classification
我们的网络学习全局点云特征，可以用于对象分类。
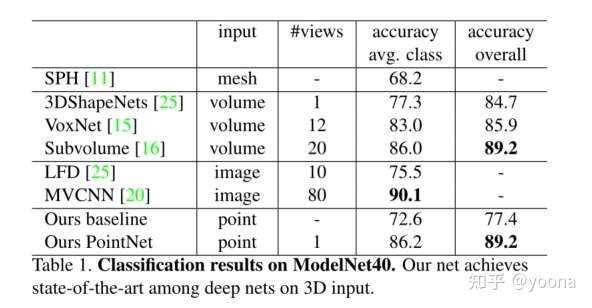
我们在ModelNet40[25]形状分类基准上对我们的模型进行了评估。有来自40个人造物体类别的12,311个CAD模型，分为9,843个训练和2468个用于测试。虽然以前的方法侧重于体积和多视图图像表示，但我们是第一个直接处理原始点云的方法。我们按照面的面积对网格面上的1024个点进行均匀采样，并将它们归一化为一个单位球体。在训练过程中，我们通过沿上轴随机旋转对象来动态增强点云，并用均值为零且标准差为0.02的高斯噪声对每个点的位置进行抖动。
在下表中，我们将我们的模型与以前的工作以及我们使用MLP从点云提取的传统特征(点密度、D2、形状轮廓等)上的基线进行了比较。
3D Object Part Segmentation
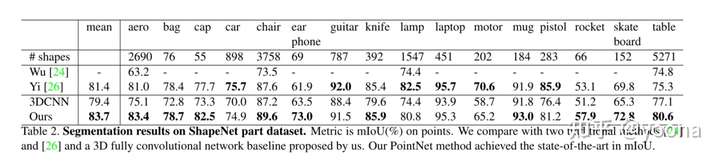
部分分割是一项具有挑战性的细粒度3D识别任务。在给定3D扫描或网格模型的情况下，任务是为每个点或面分配零件类别标签(例如椅子腿、杯柄)。我们对来自的【1】ShapeNet部件数据集进行了评估，该数据集包含来自16个类别的16,881个形状，总共标注了50个部件。大多数对象类别都标有两到五个部分。grouth-truth被设置在采样的点上。
我们将部分分割问题描述成逐点分类问题。评价指标为Miou on Points，对于C类的每个形状S，要计算该形状的mIoU值 。对于C类中的每个部件类型，计算预测值和真实值的IoU，如果基本事实和预测点的并集为空，则将部分IoU计算为1，然后，我们对C类中所有部件类型的IoU进行平均，以得到该形状的mIoU值。为了计算该类别的mIoU，我们取该类别中所有形状的mIoU的平均值
下表中，我们展示了每个类别和mIoU(%)分数。我们观察到mIoU提高了2.3%，我们的净值在大多数类别中都超过了基线方法
我们还在模拟Kinect scan上进行了实验，以测试这些方法的稳健性。对于ShapeNet零件数据集中的每一个CAD模型，我们使用Blensor Kinect Simulator 从六个随机视点生成不完整的点云。我们使用相同的网络架构和训练设置对PointNet进行完整形状和部分扫描的训练。结果表明，我们只损失了5.3%的mIoU。下图，我们给出了完整数据和部分数据的定性结果。可以看出，尽管部分数据相当具有挑战性，但我们的预测是合理的。
Semantic Segmentation in Scenes
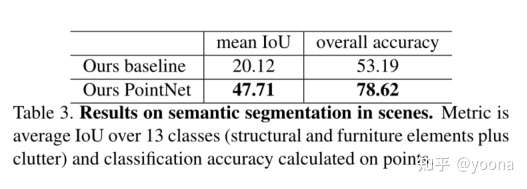
我们的网络可以很容易的扩展到场景语义分割的任务上，在此任务上，点标签变成语义对象类，而非物体的部分标签。我们在斯坦福大学3D语义分析数据集上进行了实验。该数据集包含来自Matterport扫描仪的6个区域的3D扫描，包括271个房间。扫描中的每个点都用来自13个类别(椅子、桌子、地板、墙壁等加上杂物)的一个语义标签进行注释。
为了准备训练数据，我们首先按房间划分点，然后将样本室分成面积为1m×1m的块。我们使用pointNet的segmentation 部分来预测每个块中的每个点类。每个点由9维的XYZ向量，RGB和对于房间规格化后的位置。在训练的时候，我们随机在每个区块种采样4096个点。在测试的时候，我们测试所有的点。对于训练和测试，我们使用k-fold策略。
我们将我们的方法与使用手工制作的点特征的基线进行比较。该基线提取了相同的9维局部特征和三个额外的特征：局部点密度、局部曲率和法线。我们使用标准的MLP作为分类器。结果如下表所示，其中我们的PointNet方法的性能明显优于基线方法。下图，我们显示了定性的分割结果
Reference
原文：
Qi C R, Su H, Mo K, et al. Pointnet: Deep learning on point sets for 3d classification and segmentation[C]
//Proceedings of the IEEE conference on computer vision and pattern recognition. 2017: 652-660.
【1】 L. Yi, V . G. Kim, D. Ceylan, I.-C. Shen, M. Y an, H. Su,C. Lu, Q. Huang, A. Sheffer, and L. Guibas. A
scalable active framework for region annotation in 3d shape collections. SIGGRAPH Asia, 2016
Reflection
之前因为直接看的OMnet，有挺多地方不理解的，这篇对初学者更加友好。在写的过程中也发现OMNet确实是参考了这篇文章的一些思想，比如将逐点特征和全局特征结合，使用最大池化等等。